
208
единожды обученная сеть, а в качестве входного параметра на каждом
последующем шаге используется значение, предсказанное ИНС
на предыдущем шаге. Ясно, что лучший итерационный прогноз даст
использование только одного индекса. Иначе для последующего шага
требуется прогноз и остальных. В качестве прогнозируемого индекса
используется число W как имеющее наибольший период регистрации.
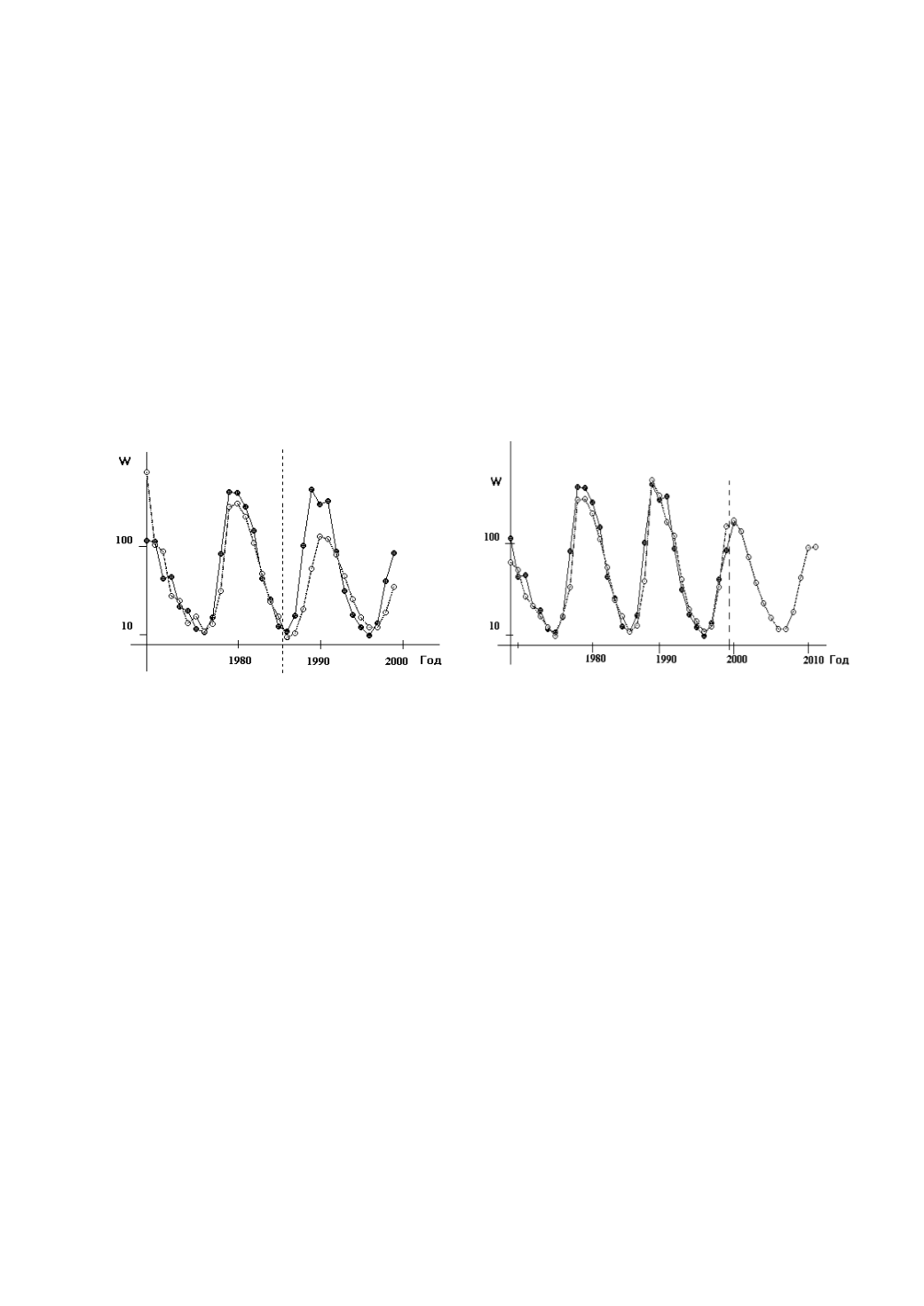
На рисунке 7.9a представлены результаты проверки качества
прогнозирования (PE= 66%) на 14 лет с 1986 г., т.е. на прошедшие годы.
На рисунке 7.9б показано реальное (настоящее) прогнозирование
среднегодового числа Вольфа на 11 лет вперед с 2000 г. В обоих случаях
осуществлялся «прогрев» ИНС по вышеупомянутой схеме.
а)
б)
Рисунок 7.9 – (а) Проверка итерационного прогнозирования на 14 лет вперед обученной
ИНС с использованием прогрева. Участок прогрева отделен от проверочного ряда
вертикальной пунктирной линией. (б) Итерационное прогнозирование на 11 лет с 2000 г.
вперед обученной ИНС с использованием прогрева. Участок прогрева отделен
от предсказания вертикальной пунктирной линией. По вертикальной оси отложены значения
среднегодового числа Вольфа (W), по горизонтальной – время в годах (белые кружки –
значения, полученные ИНС; черные кружки – реальные значения)
В ходе данного эксперимента по итерационному прогнозированию
23 цикла максимум числа солнечных пятен, как и при прямом
прогнозировании, оказался меньшим, чем значение этого максимума,
полученное на основе классического правила Гневышева-Оля. Эффект
снижения величины максимума в прогнозируемом итерационным методом
цикле может быть обусловлен и внутренней особенностью архитектуры
ИНС. Дело в том, что для уверенной работы ИНС она должна обладать
устойчивостью, что обеспечивается при итерационном прогнозировании
наличием обратной связи. Такая устойчивость приобретается ИНС
во время обучения. Она приводит к возникновению некоторой внутренней
диссипации, которая не позволяет ИНС входить в режим

















