
86
возмущение разделится на собственные волны, бегущие с различными
скоростями. Интерфейс созданной компьютерной программы позволяет
вычленить такую собственную волну и использовать ее в качестве
начальных условий для других экспериментов с такими же параметрами
среды. Таким образом, можно методами вычислительного эксперимента
исследовать
взаимодействие
и
рассеяние
магнитосферных
МГД-волн,
которое
оказывается
наиболее
интересным
при распространении волн под углом к направлению геомагнитного поля
(подробнее см. в [
Бархатов и др., 2000
]). Пример такой волновой
динамики, инициированной возмущением поперечного магнитного поля
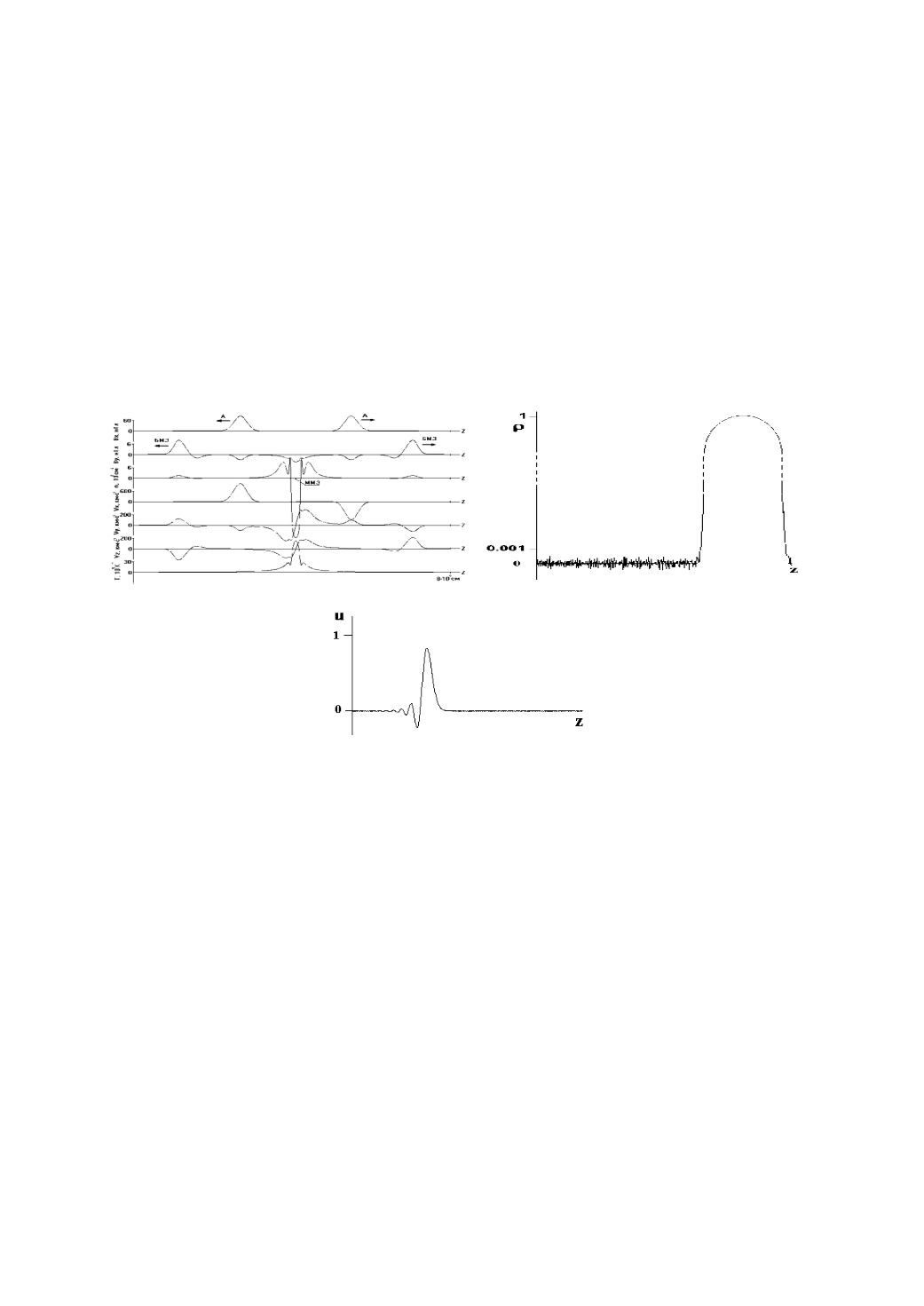
гауссовой формы, показан на рисунке 4.1а.
а)
б)
в)
Рисунок 4.1 – Распад начального пространственно локализованного возмущения
на МГД-волны (а) и искажения на хвосте распространяющегося волнового импульса,
обусловленные дискретностью времени (б) и дискретностью пространственной
переменной (в)
В последнее время широкое распространение получили численные
методики решения сложных нелинейных задач, поэтому естественно
возникает вопрос об их адекватности аналитическим решениям. Нередко
полагают, что континуальные (непрерывные) уравнения рассматриваемого
типа более точны, чем рекурсивный вычислительный алгоритм,
возникающий в результате их дискретизации. Доминирование взглядов,
что дискретная модель отличается от континуальной только «ошибками
численного счета», сложилось в докомпьютерную эпоху и, несомненно,
будет пересматриваться в ближайшие десятилетия. По поводу устойчивых
и неустойчивых разностных схем можно достаточно четко говорить только
тогда,
когда
решение
континуальной
системы
устойчиво
[
Самарский, 1977
]. Для неустойчивых решений такое понятие пропадает,

















