
23
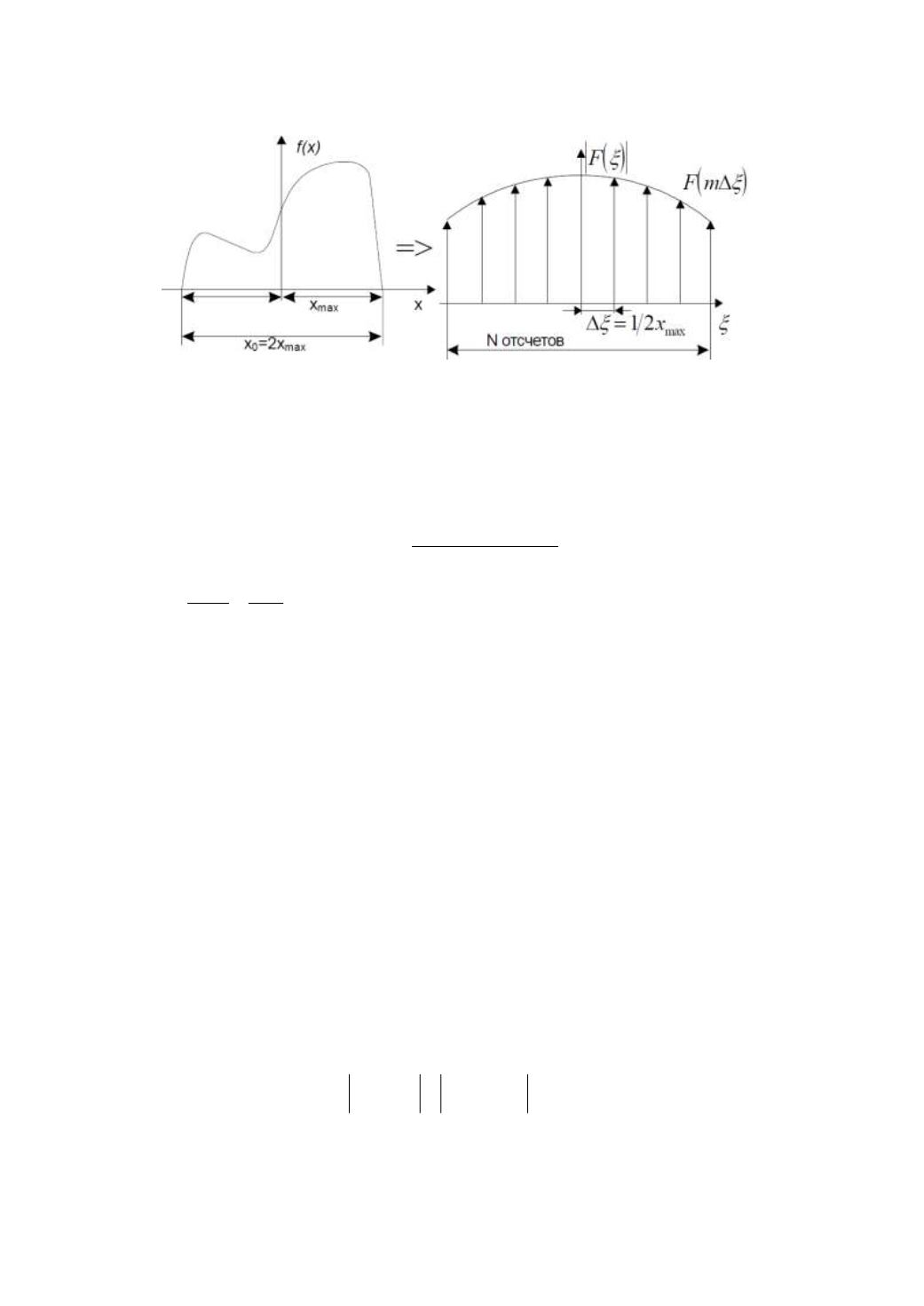
Рисунок 1.2 – Выбор шага дискретизации по теореме Котельникова
При дискретизации, согласно теореме Котельникова, исходная
функция
f(x)
может быть получена по ее дискретным значениям
по формуле:
max
max
sin 2 (
)
( )
( )
(
)
k
x k x
f x
f k x
x k x
(1.11)
где
max
max
1
2
x
.
Однако, согласно теории Фурье-анализа, конечной апериодической
функции
f(x)
соответствует бесконечный спектр, и наоборот, конечный
спектр соответствует бесконечной исходной функции. Поэтому
для реальных сигналов условия теоремы Котельникова в строгом смысле
слова не выполняются. Из теоремы следует такой вывод:
1. Все реальные сигналы ограничены во времени и имеют
неограниченный спектр.
2. В соответствии с рядом Котельникова восстановление
осуществляется по бесконечному числу отсчетов.
3. Поскольку сигнал восстанавливается по бесконечному числу
отсчетов функций, то его восстановление осуществляется с бесконечной
задержкой во времени.
Поэтому, чтобы получить конечный спектр, можно воспользоваться
равенством Парсеваля:
0
( )
( ) d (1 )
T
f t dt
F
Зная, что исходная функция
f(x)
конечна, можно вычислить значение
интеграла в левой части равенства, после чего, задав величину

















